Cálculo Integral
Este es un Blog de la materia Cáclulo Integral, impartida por el Ing. José Enrique Márquez Eloiza en el Tecnológico de Estudios Superiores de Cuautitlán Izcalli y realizado por Malinalli Ibarra Rodríguez del salón 322-M.
Traductor
lunes, 9 de julio de 2012
TEMARIO DE UNIDAD 4
4.1 Definición de serie.
4.1.1 Finita.
4.1.2 Infinita
4.2 Serie numérica y convergencia. Prueba de razón y raiz.
4.3 Serie de potencias.
4.4 Radio de convergencia.
4.5 Serie de Taylor.
4.6 Representación de funciones mediante serie de Taylor.
4.7 Cálculo de integrales de funciones expresadas como serie de Taylor.
4.1 SERIES
Una serie es una sucesión de un conjunto de términos formados según una ley determina.
Por ejemplo, 1,4,9,16,25
Es la suma indicada de los términos de una secesión. Así de las sucesiones anteriores obtenemos la serie:
1+4+9+16+25
Cuando el número de términos es limitado, se dice que la sucesión o serie es finita. Cuando el número de términos es ilimitado, la sucesión o serie se llamasucesión infinita.
El término general ó término enésimo es una expresión que indica la ley de formación de los términos.
4.1.1 FINITA
Sucesión de números tales que la proporción entre cualquier término (que no sea el primero) y el término que le precede es una cantidad fija llamada razón. Por ejemplo, la secuencia de números 2, 4, 8, 16, 32, 64, 128 es una progresión geométrica con razón 2; y 1, 1, 3, 7, 9, >, … (1)i, es una progresión geométrica con razón 1.
La primera es una progresión geométrica finita con siete términos; la segunda es una progresión geométrica infinita. En general, una progresión geométrica se puede describir utilizando la siguiente notación: a es el primer término, la razón es r y, en una progresión finita, n es el número de términos.
4.1.2 INFINITA
En un lenguaje sencillo, una serie a1+ a2+ a3+ a4… es una rreglo ordenado de número reales, uno para cada entero positiva, es una función cuyo dominio es el conjunto de enteros positivos y cuyo rango es un conjunto de números reales. Podemos indicar una sucesión mediante a1, a2, a3… mediante a(n) infinito=1, en algunos casos, extenderemos este concepto permitiendo que el dominio conste de todos los enteros mayores o iguales a un entero específico como en b1, b2, b3… y c8, c9, c10…. Que denotamos como {b(n)infinito=0} y {c(n)infinito=8, respectivamente.
Se puede especificar una sucesión dando suficientes términos iniciales para establecer un patrón como en:
1, 4, 7, 10, 13…
Mediante una fórmula explícita para el n-ésimo término, como en:
A(n)=3(n)-2, n >1
4.2 Serie numérica y convergencia. Prueba de razón y raíz.
Una
secuencia es una lista ordenada de objetos (o eventos). Como un conjunto, que
contiene los miembros (también llamados elementos o términos ), y el número de
términos (posiblemente infinita) se llama la longitud de la secuencia. A diferencia
de un conjunto, el orden importa, y exactamente los mismos elementos pueden
aparecer varias veces en diferentes posiciones en la secuencia. Una secuencia
es una discreta función.
Por ejemplo, (C, R, Y) es una
secuencia de letras que difiere de (Y, C, R), como las cuestiones de pedido.
Las secuencias pueden ser finitos, como en este ejemplo, o infinita, como la
secuencia de todos, incluso positivos enteros (2, 4, 6 ,…). secuencias finitos
se conocen como cadenas o palabras y secuencias infinitas como los arroyos. La
secuencia vacía () se incluye en la mayoría de las nociones de secuencia, pero
pueden ser excluidos en función del contexto.
Ejemplos y notacion
Hay muchas diferentes nociones de
secuencias en las matemáticas, algunas de las cuales ( por ejemplo, la
secuencia exacta ) no están cubiertos por las anotaciones que se presentan a
continuación.
Además de identificar los elementos de
una secuencia por su posición, como “la tercera elemento”, elementos que pueden
dar los nombres de referencia conveniente. Por ejemplo, una secuencia podría
ser escrito como ( un uno , un dos , un dos , …), o ( b 0 , b 1 , b 2 , …), o (
c 0 , c 2 , c 4 , …), dependiendo en lo que es útil en la aplicación.
Finito y lo infinito Una definición
más formal de una secuencia finita con los términos de un conjunto S es una
función de {1, 2, …, n } a S por alguna n > 0. Una secuencia infinita de S
es una función de {1, 2, … A} S. Por ejemplo, la secuencia de números primos
(2,3,5,7,11, …) es la función 1 →
2 , 2 → 3 , 3 → 5 , 4 →
7 , 5 → 11 , ….
Una secuencia de longitud finita n es
también llamado n -tupla; secuencias finitas incluyen la secuencia vacía () que
no tiene elementos.
Una de las funciones de todos los
números enteros es que en un conjunto a veces se denomina secuencia infinita-bi
o dos vías secuencia infinita. Un ejemplo es la secuencia bi-infinita de todos
los enteros pares (…, −4, −2, 0, 2, 4, 6, 8 …).
Multiplicativo Deja una = ( una
secuencia definida por una función f : {1, 2, 3, …} → {1, 2, 3, …}, de tal manera que un i = f (i). La secuencia es
multiplicativo si f ( xy ) = f ( x ) f ( y ) para todo x , y tales que x e y
son primos entre sí.
Criterio de D'Alembert (Criterio de la
razón)
Sea una serie
, tal que ak > 0 ( serie de términos positivos).
Si existe
con
, el Criterio de D'Alembert establece
que:
§
si L < 1, la serie converge.
§
si L > 1, entonces la serie diverge.
§
si L = 1, no es posible decir algo sobre el comportamiento
de la serie.
En este caso, es necesario probar otro criterio,
como el criterio de Raabe.
Criterio de Cauchy (raíz enésima)
Sea una serie
, tal que ak > 0 (serie de términos positivos). Y supongamos
que existe
Entonces, si:
§
L < 1, la serie es convergente.
§
L > 1 entonces la serie es divergente.
§
L=1,
no podemos concluir nada a priori y tenemos que recurrir al criterio de Raabe,
o de comparación, para ver si podemos llegar a alguna conclusión.
4.4 Radio de convergencia.
Llamamos serie de potencias a toda expresión del tipo
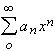 , en donde
, en donde
Es decir
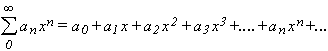
Por ejemplo
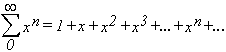
en donde todos los 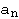 valen 1, o
valen 1, o

y todos sus 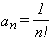 .
.
Es interesante saber cuáles son los de x Î R para los que las respectivas series funcionales se convierten en seriesnuméricas convergentes. Por ejemplo si en la primera de las dos series anteriores hacemos x=0,  es 1 + 0 + 0 +....+ 0 +... y estaserie es obviamente convergente. En si x = 1, se convierte en 1 + 1 +... +... que es divergente.
es 1 + 0 + 0 +....+ 0 +... y estaserie es obviamente convergente. En si x = 1, se convierte en 1 + 1 +... +... que es divergente.
Pero para x = 1/2 es
que es una serie geométrica de razón 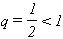 y su
y su 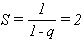 con lo que la serie es convergente. Más aún,
con lo que la serie es convergente. Más aún,  es una serie geometrica de razón x y será convergente si
es una serie geometrica de razón x y será convergente si 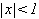 , es decir si
, es decir si 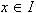 ,
,
siendo 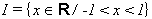 .
.
Si se cumple esta condición:
Entonces bajo ciertas condiciones, una serie de potencias describe exactamentea a una función. En este caso a 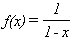 , pero sólo en el intervalo (-1;1).
, pero sólo en el intervalo (-1;1).
4.5 Serie de Taylor.
Si la función f y sus primeras n+1 derivadas son continuas, en un intervalo que contiene a y x, entonces el valor de la función esta dado por:
Con frecuencia es conveniente simplificar la serie de Taylor definiendo un paso h = xi+1 - xi expresando la serie de Taylor como:
Uso de la expansión en serie de Taylor para aproximar una función con un número infinito de derivadas.
Utilizar los términos de la serie de Taylor con n= 0 hasta 6 para aproximar la función f(x) = cos(x) en xi+1 = p/3 y sus derivadas en xi = p/4. Esto significa que h = p/3- p/4 =p/12, los valores de las derivadas y el error de aproximación se presenta en la siguiente tabla.
Orden n
|
fn(x)
|
fn(p/4)
|
error (%)
|
0
|
cos(x)
|
0.707106781
|
-41.4
|
1
|
-sen(x)
|
0.521986659
|
-4.4
|
2
|
-cos(x)
|
0.497754491
|
0.449
|
3
|
sen(x)
|
0.499869147
|
2.62x10-2
|
4
|
cos(x)
|
0.500007551
|
-1.51x10-3
|
5
|
-sen(x)
|
0.500000304
|
-6.08x10-5
|
6
|
-cos(x)
|
0.499999988
|
2.40x10-6
|
Note, que a medida que se introducen más términos, la aproximación se vuelve más exacta y el porcentaje de error disminuye. En general podemos tener una aproximación polinomial de la función coseno, con sus derivadas en cero dada por
Orden n
|
fn(x)
|
fn(0)
|
0
|
cos(x)
|
1
|
1
|
-sen(x)
|
0
|
2
|
-cos(x)
|
-1
|
3
|
sen(x)
|
0
|
4
|
cos(x)
|
1
|
5
|
-sen(x)
|
0
|
6
|
-cos(x)
|
-1
|
7
|
sen(x)
|
0
|
8
|
cos(x)
|
1
|
9
|
-sen(x)
|
0
|
10
|
-cos(x)
|
-1
|
La aproximación polinomial final queda:
4.6 Representación de funciones mediante serie de Taylor.
Teorema de Taylor. Si la función f y sus primeras n+1 derivadas son continuas en un intervalo que contiene a a y a x, entonces el valor de la función en un punto x está dado por:
Existen series de Taylor para: Función exponencial y función Coseno.
Funcion e
Se puede aplicar la ecuación de las series de Taylor como más sencillo le resulte a cada quien, una de tantas formas la explicare aquí.
Lo primero que se hace es derivar unas 3 o 4 veces la función, esto porque algunas funciones empiezan a tener un patrón repetitivo después de cierto número de derivaciones, como la función e.
Después se tiene que sustituir "a" en cada una de las derivadas, pero como se decidió que "a" era 0 se sustituye un 0 en cada derivada y se observa que resultados da.
Lo primero que se hace es derivar unas 3 o 4 veces la función, esto porque algunas funciones empiezan a tener un patrón repetitivo después de cierto número de derivaciones, como la función e.
Después se tiene que sustituir "a" en cada una de las derivadas, pero como se decidió que "a" era 0 se sustituye un 0 en cada derivada y se observa que resultados da.
f(x)=e(x).... f(o)=1
Esto de sustituir en cada derivada es solo para simplificar la ecuación de la serie y para darnos una idea de como se comporta la función. Una vez que se tiene una idea del comportamiento de la función se puede ir empezando a armar la ecuación de la serie
Con las primeras operaciones que se hicieron al principio se puede ver como se irá llenando la serie mientras más elementos se le agreguen para que el resultado sea más preciso. Todo esto fue para ver como es la serie de la función e, ahora para conocer algún resultado simplemente se sustituye en donde quedaron las x y ya está
Función Coseno
Para el coseno el procedimiento es el mismo.
Primero se deriva varias veces la función y se sustituye en valor de "a" en cada una para observar el patrón.
Primero se deriva varias veces la función y se sustituye en valor de "a" en cada una para observar el patrón.
Despues se va llenando la serie de Taylor para despues hacer una ecuacion general:
Para otras funciones continuas diferenciables, como las exponenciales o sinusoidales, no se obtiene una estimación exacta mediante un número finito de términos.El valor práctico de las series de Taylor radica en el uso de un número finito de términos que darán una aproximación lo suficientemente cercana a la solución verdadera para propósitos prácticos
Suscribirse a:
Comentarios (Atom)
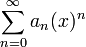
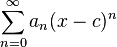
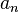 son los términos de una sucesión.
son los términos de una sucesión.


