4.4   Radio de convergencia.

Llamamos serie de potencias a toda expresión  del tipo

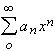, en donde 

Es decir

                 

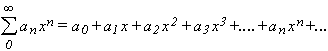
Por ejemplo

                 

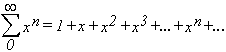
en donde todos los 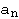valen 1, o

                 

y todos sus .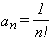

Es interesante saber cuáles son los valores de x Î R para los que las respectivas series funcionales se convierten en seriesnuméricas convergentes. Por ejemplo si en la primera de las dos series anteriores hacemos x=0, es 1 + 0 + 0 +....+ 0 +... y estaserie es obviamente convergente. En cambio si x = 1, se convierte en 1 + 1 +... +... que es divergente.

Pero para x = 1/2 es

                                   

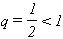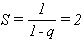que es una serie geométrica de razón y su suma con lo que la serie es convergente.   Más aún,   es una serie geometrica de razón x  y será convergente si 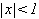, es decir  si ,

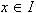siendo .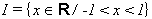

Si se cumple esta condición:

                     

Entonces bajo ciertas condiciones, una serie de potencias describe exactamentea a una función. En este caso a 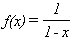, pero sólo en el intervalo (-1;1).